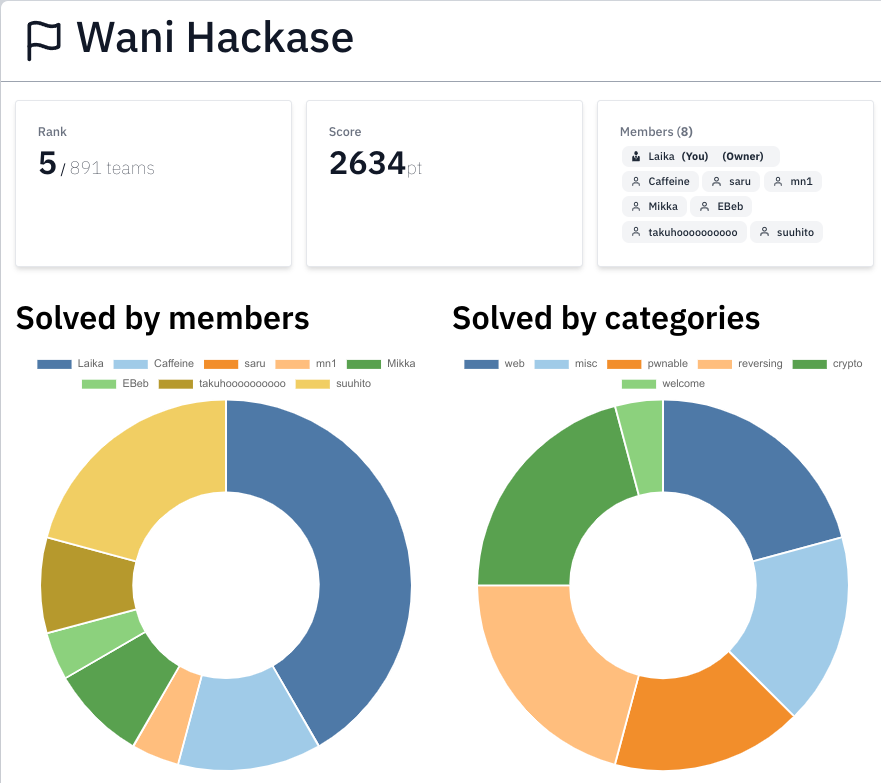
6月4日の14時から24時間開催されていたSECCON Beginners CTF 2022にWani Hackase で参戦して5位でした。 普段のreversing担当が不在だったので、reversingとcryptoを担当しました。
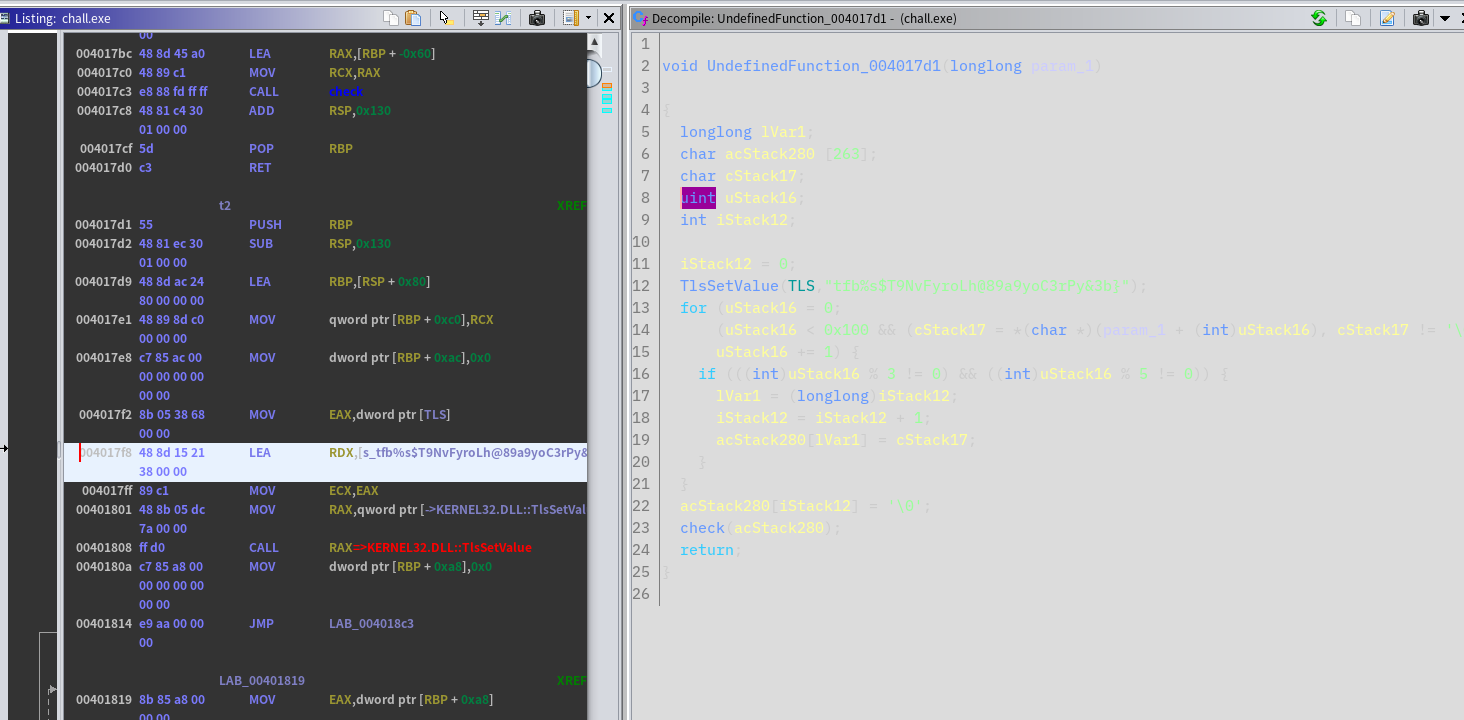
WinTLS [reversing, 102 solved]
Windowsというだけで忌避していたこの手の問題に、久しぶりに挑戦しました。
.rdataを漁っていると香ばしい文字列(c4{f..., tfb%...)があったのでxrefで参照元を見に行きます。
2つのスレッドで文字列を処理していて、flagのインデックスに応じて2つの文字列に振り分けているようです。
操作は単純なので逆の操作をしてあげると、文字列を復元できます。
1t1 = b"c4{fAPu8#FHh2+0cyo8$SWJH3a8X"
2t2 = b"tfb%s$T9NvFyroLh@89a9yoC3rPy&3b}"
3
4flag = []
5k1, k2 = 0, 0
6for i in range(len(t1+t2)):
7 if i % 3 == 0 or i % 5 == 0:
8 flag.append(t1[k1])
9 k1 += 1
10 else:
11 flag.append(t2[k2])
12 k2 += 1
13
14print(bytes(flag))
Flag: ctf4b{f%sAP$uT98Nv#FFHyrh2o+Lh0@8c9yoa98$ySoCW3rJPH3y&a83Xb}
ところで、UndefinedFunctionがめちゃくちゃ見にくい……
Recursive [reversing, 127 solved]
再帰で文字列をぐちゃぐちゃにしてあります。 少しreversingをすると文字列長が書いてあるので、処理前の文字列が処理後にどこに配置されるかが分かれば、逆操作で元に戻せます。
1from string import printable
2
3table = b"ct`*f4(+bc95\".81b{hmr3c/}r@:{&;514od*<h,n'dmxw?leg(yo)ne+j-{(`q/rr3|($0+5s.z{_ncaur${s1v5%!p)h!q't<=l@_8h93_woc4ld%>?cba<dagx|l<b/y,y`k-7{=;{&8,8u5$kkc}@7q@<tm03:&,f1vyb'8%dyl2(g?717q#u>fw()voo$6g):)_c_+8v.gbm(%$w(<h:1!c'ruv}@3`ya!r5&;5z_ogm0a9c23smw-.i#|w{8kepfvw:3|3f5<e@:}*,q>sg!bdkr0x7@>h/5*hi<749'|{)sj1;0,$ig&v)=t0fnk|03j\"}7r{}ti}?_<swxju1k!l&db!j:}!z}6*`1_{f1s@3d,vio45<_4vc_v3>hu3>+byvq##@f+)lc91w+9i7#v<r;rr$u@(at>vn:7b`jsmg6my{+9m_-rypp_u5n*6.}f8ppg<m-&qq5k3f?=u1}m_?n9<|et*-/%fgh.1m(@_3vf4i(n)s2jvg0m4"
4
5FLAG_LEN = 0x28
6t = printable[: FLAG_LEN - 2]
7flag = [0 for _ in range(FLAG_LEN)]
8
9def check(s, i):
10 n = len(s)
11 if n == 1:
12 flag[t.index(s)] = table[i]
13 return
14 else:
15 m = n // 2
16 check(s[:m], i)
17 check(s[m:], m * m + i)
18
19check(t, 0)
20print(bytes(flag))
Flag: ctf4b{r3curs1v3_c4l1_1s_4_v3ry_u53fu1}
Ransom [reversing, 61 solved]
普段reversingをしなさすぎてRC4に気づかず、愚直にreversingしました。please_not_debug_meを解いているときに、RC4であったことに気づきました。
1def key_schedule(seed):
2 key = [i for i in range(0x100)]
3
4 j = 0
5 for i in range(0x100):
6 x = key[i] + j + seed[i % len(seed)]
7 y = (x >> 0x1F) >> 0x18
8 j = (x + y & 0xFF) - y
9 key[i], key[j] = key[j], key[i]
10
11 return key
12
13
14def decrypt(key, ciphertext):
15 n = len(ciphertext)
16 super_secret = [0 for _ in range(n)]
17 j, k = 0, 0
18 for i in range(n):
19 j = j + 1 & 0xFF
20 k = key[j] + k & 0xFF
21 key[j], key[k] = key[k], key[j]
22
23 super_secret[i] = ciphertext[i] ^ key[key[j] + key[k] & 0xFF]
24
25 return super_secret
26
27
28seed = b"rgUAvvyfyApNPEYg" # Get from tcpdump.pcap
29ciphertext = b"\x2b\xa9\xf3\x6f\xa2\x2e\xcd\xf3\x78\xcc\xb7\xa0\xde\x6d\xb1\xd4\x24\x3c\x8a\x89\xa3\xce\xab\x30\x7f\xc2\xb9\x0c\xb9\xf4\xe7\xda\x25\xcd\xfc\x4e\xc7\x9e\x7e\x43\x2b\x3b\xdc\x09\x80\x96\x95\xf6\x76\x10" # Get from ctf4b_super_secret.txt.lock
30key = key_schedule(seed)
31flag = decrypt(key, ciphertext)
32print(bytes(flag))
Flag: ctf4b{rans0mw4re_1s_v4ry_dan9er0u3_s0_b4_c4refu1}
please_not_debug_me [reversing, 48 solved]
b"\x16"でXORする簡単なpackingが施されていたので、よしなにunpackします。 unpack後はほとんどRansomと同じで、keyと暗号化後の文字列があるのでRC4で戻してあげます。
1from Crypto.Cipher import ARC4
2
3key = b"\x62\x31\x34\x62\x65\x37\x60\x32\x69\x3c\x68\x6f\x6a\x3b\x6d\x6e\x71\x26\x23\x2b\x23\x2d\x21\x24\x2c\x2f\x2f\x78\x79\x24\x29\x2f\x44\x11\x16\x45\x10\x10\x1f\x43"
4
5enc = b"\x27\xd9\x65\x3a\x0f\x25\xe4\x0e\x81\x8a\x59\xbc\x33\xfb\xf9\xfc\x05\xc6\x33\x01\xe2\xb0\xbe\x8e\x4a\x9c\xa9\x46\x73\xb8\x48\x7d\x7f\x73\x22\xec\xdb\xdc\x98\xd9\x90\x61\x80\x7c\x6c\xb3\x36\x42\x3f\x90\x44\x85\x0d\x95\xb1\xee\xfa\x94\x85\x0c\xb9\x9f\x00"
6
7key = bytearray(key)
8for i in range(0x28):
9 key[i] ^= i
10key = bytes(key)
11
12cipher = ARC4.new(key)
13message = cipher.decrypt(enc)
14print(message)
Flag: ctf4b{D0_y0u_kn0w_0f_0th3r_w4y5_t0_d3t3ct_d36u991n9_1n_L1nux?}
CoughingFox [crypto, 443 solved]
平方数かどうかを判定しながら、$i$を総当たりすればOKです。
1import ast
2from math import isqrt
3
4with open("output.txt") as f:
5 cipher = ast.literal_eval(f.readline().split("=")[-1])
6
7
8n = len(cipher)
9pos = [0 for _ in range(n)]
10
11for c in cipher:
12 for i in range(n):
13 root = isqrt(c - i)
14 if root ** 2 == c - i:
15 pos[i] = root - i
16
17print(bytes(pos))
Flag: ctf4b{Hey,Fox?YouCanNotTearThatHouseDown,CanYou?}
PrimeParty [crypto, 58 solved]
flagのビット長が与えられており、素数を好きに決められることから、平文よりでかい素数$p$を入れれば、$\mod p$ 上でのRSAとみなすことができます。
このテクニック(?)を知ったのはCrypto CTF 2020のThree Ravensが最初だったと記憶しています。 あまり直感的ではないですが、式を追えばそれもそうだなという気持ちになります。
1from Crypto.Util.number import getPrime, long_to_bytes
2from pwn import *
3
4_r = remote("primeparty.quals.beginners.seccon.jp", 1336)
5
6p = getPrime(512)
7_r.sendlineafter(b"> ", str(p).encode())
8_r.sendlineafter(b"> ", b"1")
9_r.sendlineafter(b"> ", b"1")
10_r.recvline()
11_r.recvline()
12
13n = int(_r.recvline().decode().strip().split(" = ")[-1])
14e = int(_r.recvline().decode().strip().split(" = ")[-1])
15c = int(_r.recvline().decode().strip().split(" = ")[-1])
16
17n %= p
18c %= p
19
20d = pow(e, -1, p - 1)
21m = pow(c, d, p)
22print(long_to_bytes(m))
Flag: ctf4b{HopefullyWeCanFindSomeCommonGroundWithEachOther!!!}
Command [crypto, 88 solved]
IVを好きなように書き換えられるので、bit-flippingで改竄してgetflagにします。
1from Crypto.Util.Padding import pad
2from pwn import *
3
4_r = remote("command.quals.beginners.seccon.jp", 5555)
5
6
7def encrypt_command(command):
8 _r.sendlineafter(b"> ", b"1")
9 _r.sendlineafter(b"> ", command)
10 enc = _r.recvline().decode().strip().split(": ")[-1]
11 return bytearray(bytes.fromhex(enc))
12
13
14def execute(enc):
15 _r.sendlineafter(b"> ", b"2")
16 _r.sendlineafter(b"> ", enc.hex())
17
18
19a = b"fizzbuzz"
20b = b"getflag"
21enc = encrypt_command(a)
22a, b = map(lambda x: pad(x, 16), (a, b))
23
24for i in range(0x10):
25 enc[i] ^= a[i] ^ b[i]
26
27execute(bytes(enc))
28print(_r.recvline())
Flag: ctf4b{b1tfl1pfl4ppers}
Unpredictable Pad [crypto, 35 solved]
入力チェックが負数を考慮していないので、これを利用して内部状態を32 [bit] * 624 = 19968 [bit]取得します。 あとはメルセンヌ・ツイスタを復元するツールに任せてOTPを復元してあげます。
1from Crypto.Util.number import long_to_bytes
2from mt19937predictor import MT19937Predictor # https://github.com/kmyk/mersenne-twister-predictor
3from pwn import *
4
5predictor = MT19937Predictor()
6
7
8_r = remote("unpredictable-pad.quals.beginners.seccon.jp", 9777)
9
10bits = 32 * 624
11input_to_oracle = -(2 ** bits)
12
13# Get oracle
14_r.sendlineafter(b": ", str(input_to_oracle).encode())
15oracle = int(_r.recvline().decode().strip().split(": ")[-1])
16_r.sendlineafter(b": ", b"hoge")
17_r.sendlineafter(b": ", b"hoge")
18
19encrypted_flag = int(_r.recvline().decode().strip().split(": ")[-1])
20
21# Recover the internal state of PRNG
22oracle = oracle & (2 ** bits - 1)
23predictor.setrandbits(oracle, bits)
24predictor.getrandbits(32)
25
26otp = predictor.getrandbits(encrypted_flag.bit_length())
27
28flag = encrypted_flag ^ otp
29print(long_to_bytes(flag)) # Success once every three or four times ...
Flag: ctf4b{M4y_MT19937_b3_w17h_y0u}
omni-RSA [crypto, 14 solved]
普通のRSAのパラメータに加えて $s = \left(d \mod (q-1)(r-1) \right) \mod 2^{470}$ と、$r_q = r \mod q$ が与えられています。
ここで、$s$が少し扱いづらいので、
$$
\begin{align}
d_0 := d \mod (q-1)(r-1) = 2^{470}\hat{s} + s \
\end{align}
$$
としておきます。$d_0$がだいたい512bitなので、$\hat{s}$は 512 - 470 = 42 bit くらいです。
また、$r \approx q$であるので、
$$
\begin{align}
r = q + r_q
\end{align}
$$
となります。
ここで$k \in \mathbb{Z}$を用いると、
$$ ed_0 = 1 + k(q-1)(r-1) $$
が成り立ち、さらに式(1), (2)を代入して$\mod q$をとると、 $$ \begin{align} e(2^{470}\hat{s} + s) \equiv 1 + k(-1)(r_q-1) \mod q \nonumber \\ e(2^{470}\hat{s} + s) + 1 - k(r_q-1) \equiv 0 \mod q \nonumber \end{align} $$
となります。
$k$は$e$以下を探索すれば良いので、未知数は$\hat{s}$のみとなりますが、これは42bitで比較的小さいです。
small_roots()で解けそうなので解きます。
betaの設定は、$q$が$n$のビット数のだいたい1/4=0.25なので、少し余裕を持って0.2に設定しています。
この時点で$d_0$が求まっているので、$e, d_0$が($\varphi(n)$の倍数が)わかっていることを利用して素因数分解ができます。 ここでは$p$と$qr$が出てくるので、$qr$を更に素因数分解します。 これは式(2)を使うと
$$ qr = q(q+r_q) = q^2+r_qq $$
と、二次方程式になるのでこれを解けば$p, q, r$全て求まります。
1import gmpy2
2from Crypto.Util.number import long_to_bytes
3from sage.all import *
4from tqdm import trange
5
6
7def factorize_from_kphi(n, kphi):
8 r = (kphi & -kphi).bit_length() - 1
9 s = kphi >> r
10 g = 1
11 while g := int(gmpy2.next_prime(g)):
12 x = pow(g, s, n)
13 for _ in range(r):
14 p = gcd(x - 1, n)
15 if p != 1 and p != n:
16 return p
17 x = x * x % n
18 return None
19
20
21def find_upper_d():
22 for k0 in trange(1, e + 1):
23 f = e * (x * 2 ^ kbits + s) - 1 + k0 * (rq - 1)
24 f = f.monic()
25 X = f.small_roots(X=2 ^ 42, beta=0.2)
26 if X:
27 return X[0]
28 return None
29
30
31rq = 7062868051777431792068714233088346458853439302461253671126410604645566438638
32e = 2003
33n = 140735937315721299582012271948983606040515856203095488910447576031270423278798287969947290908107499639255710908946669335985101959587493331281108201956459032271521083896344745259700651329459617119839995200673938478129274453144336015573208490094867570399501781784015670585043084941769317893797657324242253119873
34s = 1227151974351032983332456714998776453509045403806082930374928568863822330849014696701894272422348965090027592677317646472514367175350102138331
35cipher = 82412668756220041769979914934789463246015810009718254908303314153112258034728623481105815482207815918342082933427247924956647810307951148199551543392938344763435508464036683592604350121356524208096280681304955556292679275244357522750630140768411103240567076573094418811001539712472534616918635076601402584666
36
37kbits = 470
38
39# Step 1: Recover s_
40P = PolynomialRing(Zmod(n), "x")
41x = P.gen()
42
43s_ = find_upper_d()
44d0 = 2 ^ kbits * s_ + s
45kphi = int(e * d0 - 1)
46qr = int(factorize_from_kphi(n, kphi))
47p = n // qr
48
49
50# Step 2: Factorize pqr to p, q, r
51P = PolynomialRing(ZZ, "x")
52x = P.gen()
53f = x * x - rq * x - qr
54q = f.roots()[0][0]
55r = n // p // q
56
57phi = (p - 1) * (q - 1) * (r - 1)
58d = pow(e, -1, phi)
59m = pow(cipher, d, n)
60m = long_to_bytes(int(m))
61print(m)
Flag: ctf4b{GoodWork!!!YouAreTrulyOmniscientAndOmnipotent!!!}

おっぶぇ!(終了約15分前)